Accidentally Exponential Behavior in Spark

June 18, 20217 min read

At Heap, we use Apache Spark to power our Heap Connect product. This part of our system is tasked with moving large amounts of data quickly to our customers' warehouses. Using Spark allows us to easily scale up our data processing to support our largest customers, and we also get out-of-the-box support for column-based file formats like ORC.

This blog post covers one of the first performance hurdles we had to solve. Our data processing job was seemingly hanging for some of our customers. Our root cause analysis identified a slowness in the Spark implementation of the ORC file reader.

An unexpected algorithmic gotcha caused a tree-processing algorithm to perform an exponential number of operations. This meant that even a tiny tree with 50 nodes could cause the algorithm to effectively go on indefinitely.

Luckily, we managed to work around the problem on our side without depending on Spark for a fix. After fixing our immediate production issue, we also contributed to a fix for Spark.

Trees? I thought you said “customer data”

Our customers care about users, events (the actions users take on their website or product), and sessions. They also care about filtering these entities. For example, they might be interested in the “count of all events which happened in the United Kingdom.”But what if they’re interested in all events that:

happened in the United Kingdom?
were performed on a mobile device?
occurred between 5 and 7 p.m.?

It turns out that a very natural way to represent this set of predicates is with a binary tree, like this one:

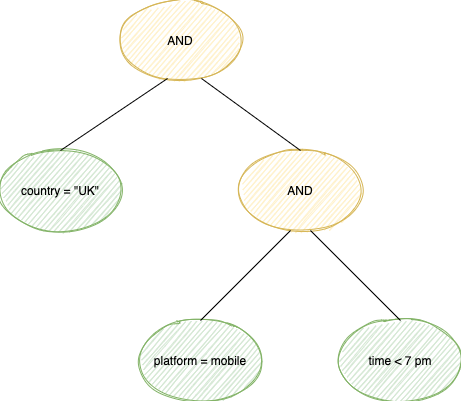
The leaf nodes represent individual filter conditions, like “country = UK”. Non-leaf nodes represent an operation performed on their subtrees. An AND node says “only match data that conforms to the conditions in my left subtree and in my right subtree”. An OR node would be similar, but matching either the left or right subtree without requiring both subtrees to match at the same time.

I mentioned “trees with 50 nodes” earlier. Does anyone really want to apply that many filters to their data? A standard situation that causes this is if the customer wants to filter for events which:

Happened in the UK, OR
Happened in the US, OR
Happened in Australia, OR
... 47 more countries.

Expressing this in a straightforward way, without introducing array-based filters, requires a tree with 50 leaf nodes.

An innocent-looking tree algorithm

Now that we’ve covered how trees come into the picture, let’s discuss why processing them can require so much time.

Although it’s a standard practice to represent filters as trees, there’s no single, widely accepted implementation. Thus, a large project like Spark might need to support and integrate with multiple such tree-based representations. In our case, some debugging pointed us towards an algorithm for converting from Spark’s internal tree-based filter into an ORC-specific SearchArgument.

Since the two formats are not 100% equivalent, the conversion had to check whether the input tree could be converted before actually attempting to do so. This resulted in code like this:

At first, this looked pretty reasonable. However, the methods canTransform and transform contain almost identical logic. Thus, in the spirit of code reuse, the implementation did this instead:

Still looking pretty reasonable. However, notice the minor, yet very important difference: we’re calling the transform method twice.

Why would that be very important? Doing something twice instead of only once sounds sub-optimal, but shouldn’t really be that bad. Right...?

Analyzing complexity

A more careful look shows that we’re not simply “doing something twice”. Instead, it’s closer to “doing something twice; then twice again, in each of these two invocations; then twice again, ...” and so on. That is, we’re “doing something twice”, raised to the power of H (where H is the height of the tree).

Let’s take a slightly more formal look. Let’s call the number of operations required to transform a tree of height H, f(H). Then:

Or, translated back into words again, the complexity of the transform function is exponential in the height of the tree being transformed.

For a tree with height 45, we get f(45) = 2 ^ 44 * f(1) = 17,592,186,044,416 * f(1).

For simplicity, let’s assume that f(1) = 1. Assuming a modern CPU can run ~3 billion operations per second, this innocent-looking tree transformation would take ~ 5800 seconds, or about an hour and a half. Each additional layer in the tree makes the operation take 2x longer.

Also, notice that 1.5 hours is the time it takes us to simply transform a filter expression from one tree format into another. Once. No customer data was analyzed during that 1.5-hour period. That part is yet to begin.It’s also interesting to note where this time is being spent. When running a Spark job, all the actual data processing is done by Spark Executors. Thus, most of the standard monitoring and optimization approaches are largely focused on Executor performance. But in our case, nothing was showing up anywhere in the Executor performance metrics. It seemed like the Executors were just idling all the time.

While Spark Executors are responsible for the data processing, the Spark Driver is the component responsible for query planning. The exponential algorithm above was part of query planning. Thus, its slowness meant that the Spark Driver never managed to successfully plan the query. Because of this, there was no work for the Executors to pick up — and, thus, they were idling.

Workaround: prefer shallow trees

When introducing the problem, I said the algorithm was “exponential in the size of the tree”. However, our more careful analysis reveals that it’s not in the size of the tree, but rather, it’s in the height of the tree that it’s exponential. We can use that detail to build a workaround.

Before we do that, let’s see how we ended up with trees that are so deep. It’s actually very easy to do so if you’re not actively trying to avoid it. In our case, we had code that looked like this:

This code was very easy to read and write. However, given a long list of andPredicates, it resulted in heavily skewed trees.

Given a list of 45 "country = X", this straightforward implementation results in a tree with depth 45 that immediately triggers the exponential behavior. This causes jobs to get stuck on the predicate conversion step.

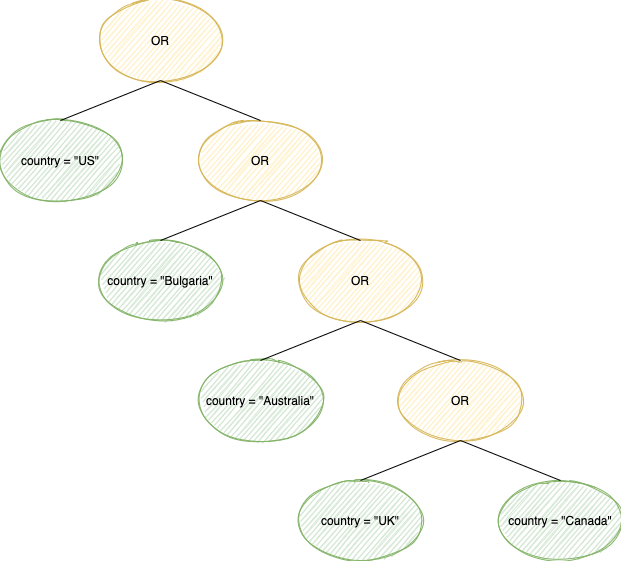
Luckily, in our specific use-case, very deep trees always had the same operation. For example, we could have a tree with 45 OR nodes like the above, or with 45 AND nodes. However, we never created 45-layer-deep trees that had a mix of ANDs and ORs. This consistency allowed us to manipulate the tree freely, without worrying about accidentally changing the semantics.

This is because, due to associativity, we can combine the AND sub-clauses however we want. We can create a subtree composed of a subset of the AND clauses, and then merge them together, thus preserving the result.

This allowed us to create an equivalent predicate tree that had a different shape. Building a balanced tree from an array of elements is a relatively standard tree algorithm. Using that instead of the heavily right-skewed tree resulted in enormous performance gains, with the performance going from multiple hours (or never finishing, for larger tree) to taking seconds.

The algorithm looks like this:

Deploying this change to our production jobs made all the performance issues related to this code go away. We didn't need to wait for a Spark release or fork the codebase in order to change Spark internals, which was great for our velocity in getting a fix out.

However, we knew that the right thing to do was to remove the exponential algorithm from Spark altogether, so we tackled that next.

Contributing back to Spark itself

We contributed a fix for the exponential complexity to Spark in: [SPARK-27105][SQL] Optimize away exponential complexity in ORC predicate conversion by IvanVergiliev · Pull Request #24068 · apache/spark. It was included in the Spark 3.0 release: ( Spark Release 3.0.0 | Apache Spark ).

The high-level idea for avoiding the exponential behavior completely was more or less clear — don't call into the same method for "checking for transformability" and "performing the transformation". Making the two different actions go through different code paths avoids the "doing something twice, recursively" problem we covered above.

Getting to a code structure that is readable and maintainable and everyone is happy with took a bit longer though. After a number of different iterations, and incorporating ideas from multiple people, we ended up with code that is both readable and performant.

If you like to solve production performance issues with algorithmic optimizations, and to improve the underlying tools you're using, we are hiring! Learn more about the awesome people on our Engineering team.

A binary tree with an "and" predicate

A binary tree with a skewed predicate